The goal of the scheduling component is to
schedule flexible energy demand and supply in the form of flex-offers.
Overview
The scheduling component is invoked each time there is a significant change in the forecasts or in the pool of aggregated flex-offers. It tries to find the best schedule for the given aggregated flex-offers by taking into account the forecast energy production and consumption and the possibility of selling energy to (and buying energy from) the market (other BRPs).
More specifically, scheduling consists of fixing start times and energy flexibilities of all given flex-offers and setting the amount of energy that will be sold to (and bought from) the market, while optimizing the total cost of the resulting schedule. The schedule cost is calculated as the sum of:
- costs of remaining mismatches,
- costs of all given aggregated flex-offers and
- costs of energy sold to (and bought from) the market.
The lower the cost, the better the schedule. Only schedules that respect all flex-offer constraints are considered.
The Mirabel scheduling problem differs from the scheduling problems treated in the literature either in the context of production systems or energy sector. Unlike the usually scheduled activities, flex-offers are structured. In addition to the start time, flex-offer and market energy amounts need to be determined, which substantially increases the problem complexity in terms of the number of candidate solutions. Furthermore, the objective function is not related to a time measure, but is rather a composed cost function. Finally, flex-offer constraints contribute to the problem specificity. These characteristics and the expected large number of flex-offers to be processed make the Mirabel scheduling problem non-standard and highly complex.
Details
Scheduling problem formulation
While scheduling in Mirabel is an optimization problem with the objective of balancing energy supply and demand, the exact formulation of the schedule evaluation function deals with the schedules from the point of view of expenses for the BRP. Such a formulation allows us to weight the remaining mismatches according to their costs (mismatches at peak periods cost the BRP more than at other periods) and differentiate among flex-offers and among market energy with different prices.
Investigation
of schedule optimality
When solving any optimization problem it is
advantageous to know its optimal solution (so an assessment of the distance to
the optimum can be computed). Because energy amounts can take on an infinite
number of values and flex-offer energy constraints construct dependences among
different intervals of a single flex-offer profile, an infinite number of
possible solutions may exist and thus the optimal solution of this problem is generally
not known. Only if a few flex-offers need to be scheduled or if there are no
flex-offer energy constraints, it is possible to find the true optimum. In a
preliminary experiment with 10 flex-offers without energy constraints it took
almost three hours to explore all (almost 850 million) sensible solutions and
find the optimal schedule.
Implementation
of the scheduling algorthms
As known scheduling heuristics cannot be applied to this problem, we used two stochastic metaheuristic algorithms to solve it:
randomized greedy search and an evolutionary algorithm. The randomized greedy search constructs the
schedule gradually-at each step a randomly chosen flex-offer is scheduled in
the best possible position. This is repeated until all flex-offers have been
scheduled. While it is possible to schedule a single flex-offer in an optimal
way, a sequence of such optimal placements does not produce an overall optimal
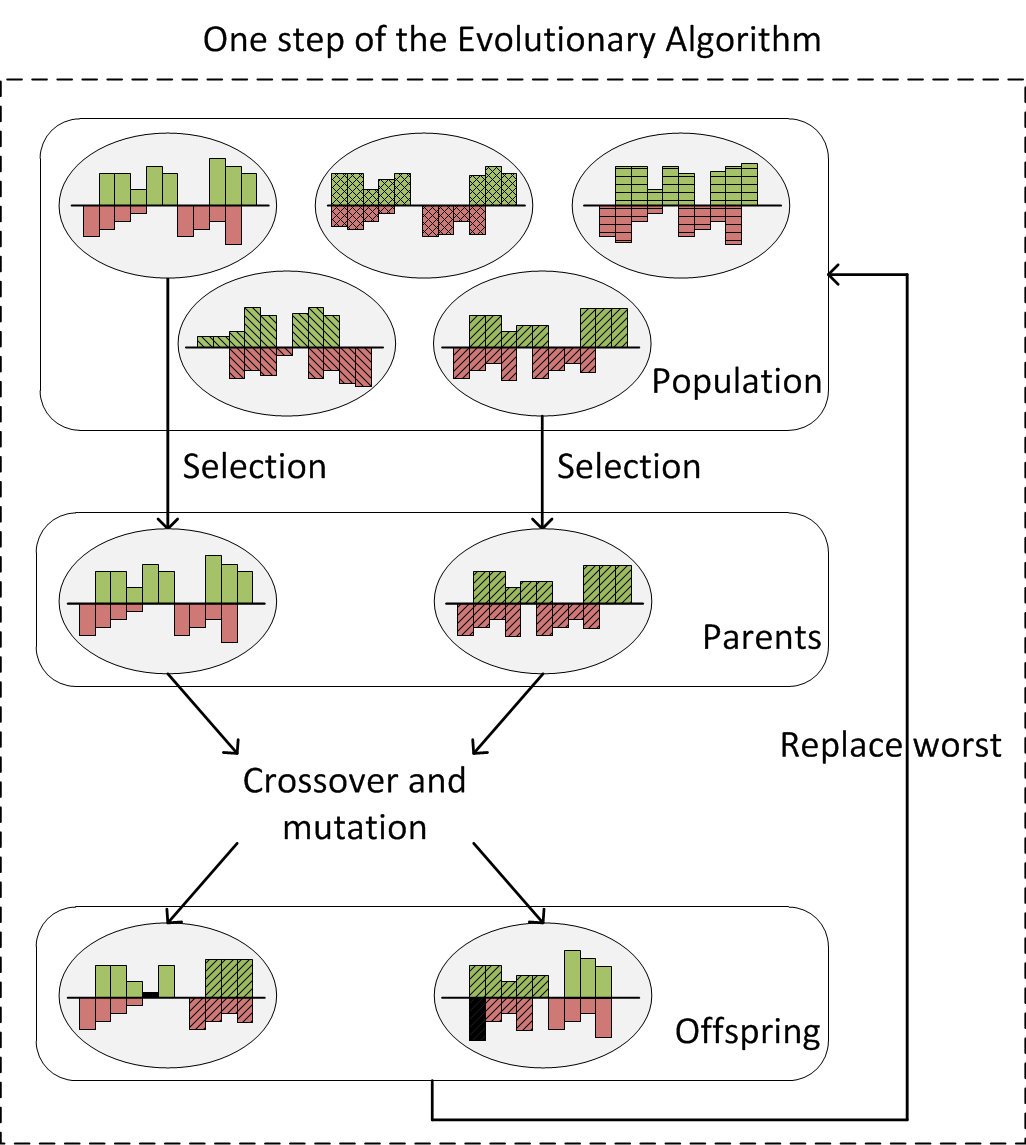
schedule. Therefore, we also developed an evolutionary
algorithm that starts with a population of randomly created solutions and
uses evolutionary principles of selection, crossover and mutation to find
progressively better solutions as shown in the figure below.